Malaria model general information

Here we describe the broad overview of how the malaria model functions. As there are numerous parameters in the model, it is useful to categorize parameters into components, which are described in the Malaria model structure and framework section.

The core of the simulation consists of solvers for mosquito population dynamics, pathogen transmission to and from the human host population, and dynamics of the infection within the human host. While the human population is fully individual-based, the mosquito population can be represented by discrete cohorts or individual agent mosquitoes. As an agent-based model, interactions between humans and vectors advance during each time step. The mosquito population is advanced, for example, through discrete 1-day time steps during which mosquitoes may engage in host- seeking or feeding behaviors, mating, maturation through a life-stage, or even death. Successful feeds on humans can result in infection of the human host, or conversely, susceptible mosquitoes may become infected from an infectious human.

Model implementation structure

There are two categories of possible implementations of the basic model, each with different computational efficiencies, resolutions, and flexibilities. The first is an individual model, where it simulates every individual mosquito in the population or can utilize a sampled subset of mosquitoes to represent the population as the whole. The second is a modified cohort simulation, with or without explicit mosquito ages.

Individual mosquito model

This basic model can be implemented through simulation of every individual mosquito, or by simulation of a subset of individual mosquitoes to represent the full population. Each mosquito’s state contains status (susceptible, latently infected, and infectious), timers for transition to adult from immature and infected to infectious, mating status and Wolbachia infection, and age. An oviposition timer to enforce a fixed feeding cycle may be included as well. If mosquitoes are sampled and a subset used to represent the local population, each sampled mosquito will have an associated sampling weight as well.

Cohort model

In the modified cohort simulation, rather than representing the entire population by three compartments for susceptible, latently infected, and infectious mosquitoes, the simulation dynamically allocates a cohort for every distinct state, and the cohort maintains the count of all mosquitoes in that state. This allows temperature-dependent progression through sporogony, even with a different mean temperature each day, with no mosquitoes passing from susceptible to infectious before the full discrete latency. For the cohort simulation with explicit ages, in order to allow modeling of senescence, mosquito age is part of the state definition, and many more cohorts are required to represent the population.

Discrete and continuous processes

The model implements a hybrid of discrete and continuous processes that work together to capture system latencies and discrete events inherent in the population dynamics of humans, mosquitoes, and parasites. Discrete events, such as latencies in the infected hepatocyte stage, the length of the asexual cycle from merozoite invasion to schizont rupture, and gametocyte maturation have particular time durations. State changes occur after the completion of the required amount of time (with specific time durations set for each state). See the figure of the Plasmodium life-cycle in Malaria disease overview for more information regarding the life-cycle stages used in this example.

Other processes, such as the decay of antibodies and the clearance of parasites, are represented by continuous-time processes. These are solved with a one-hour time step Euler method. All parasite quantities, such as the number of hepatocytes, number of merozoites, number of infected red blood cells of each antigenic variant, and gametocytes of each stage are represented as discrete integers. The infection is not cleared until each category is reduced to zero. This allows resolution of model dynamics at subpatent levels.

Spatial-scale dynamics and migration

Extensive multi-node simulations with location-specific climate, intervention deployments, larval habitat, and migration may be configured within the EMOD framework. Nodes can be configured to best represent the spatial scale being simulated: a node can be the household level, village level, county level, country level, or other desired geographic scale. Migration can be enabled between nodes, such that EMOD can most accurately represent the dynamics of the location. By varying spatial-scale resolution, relevant factors for transmission dynamics can be more clearly elucidated.

The following visualization shows an example of a gridded representation of malaria transmission on the island of Madagascar.

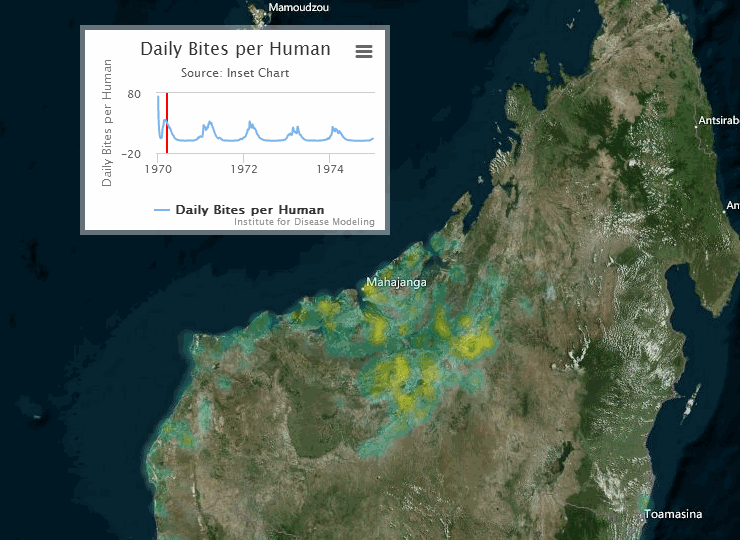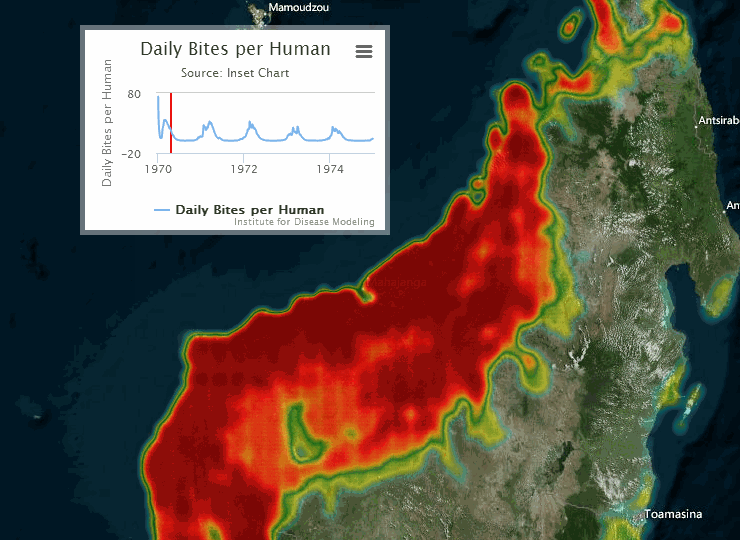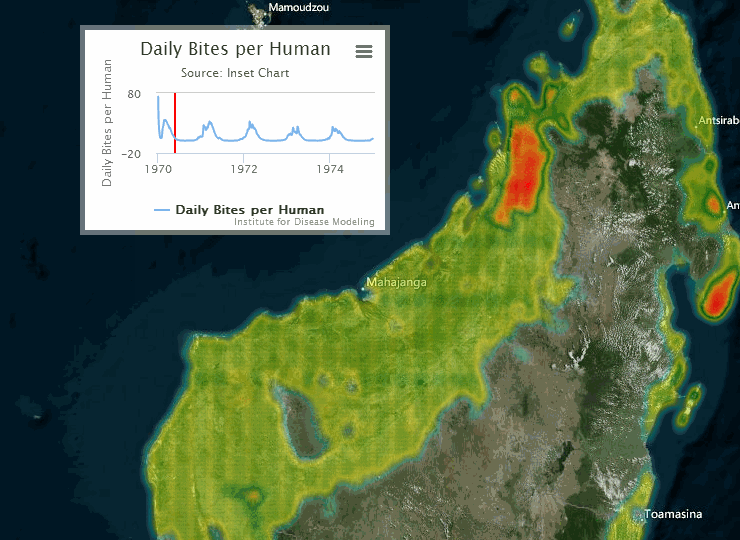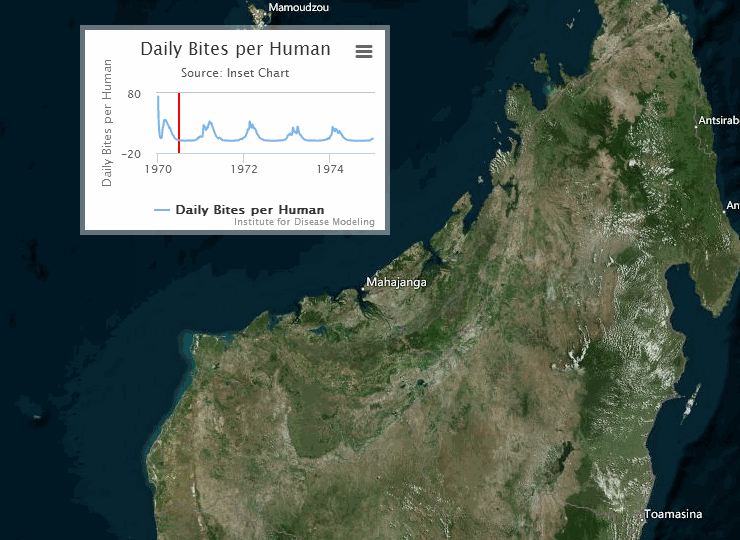
For information on configuring nodes and migration parameters, see Migration file structure.