Introduction to disease modeling¶
To understand the complex dynamics underlying disease transmission, epidemiologists utilize a set of models called compartmental models. Developed in the early 20th century, these models stratify a population into groups, generally based on their risk or infection status. Underlying these models is a system of differential equations, so the model is able to track the population as a function of time. Further, the models track the number of people in each category, are able to predict the various properties of pathogen spread, can estimate the duration of epidemics, and can be used to understand how different situations or interventions can impact the outcome of pathogen spread. To see a typical plot of a population in SIR conditions, see the plot in Types of compartmental models. If you would like a more in-depth introduction to epidemiology and disease modeling, you may want to take the Epidemics course from The Pennsylvania State University through Coursera.
An agent-based model (ABM) is another powerful tool used to help understand the complexity inherent in disease transmission systems. These models form a type of “microscale model,” where they simulate the simultaneous interactions of agents in an effort to re-crate complex phenomena. Each agent (such as a human, or vector) can be assigned a variety of “properties” (for example, age, gender, etc), and their behavior and interactions with one another are determined by using decision rules. These models have strong predictive power, and are able to leverage spatial and temporal dynamics. Further, complex environments can be developed in which the agents act, and agents may “learn” from interactions or “adapt” to their environment. As a result, ABMs are excellent for identifying “emerging properties” of the system: patterns that are not explicitly modeled, but instead occur as a consequence of the rules that govern the agents.
Agent-based models are extensively used in epidemiology due to their predictive power in modeling the spread (or conversely, control) of epidemics. A popular type of ABM for this is one in which each agent’s rules follow the dynamics specified in the compartmental models, where each agent flows through the compartments as a function of both “within-host” rules (such as duration of infection) and interactions between agents (such as becoming infected when coming into contact with an infectious agent). By combining the epidemiological basis of compartmental models with the flexibility of an agent-based model, this type of ABM is quite powerful due to their ability to simultaneously address the ecology, epidemiology, and pathology of complex systems.
Why use disease modeling¶
Disease models play an important role in understanding and managing the transmission dynamics of various pathogens. We can use them to describe the spatial and temporal patterns of disease prevalence, as well as to explore or better understand the factors that influence infection incidence. Modeling is a key step in understanding what treatments and interventions can be most effective, how cost-effective these approaches may be, and what specific factors need to be considered when trying to eradicate disease.
Types of compartmental models¶
The following diagrams illustrate common compartmental models.
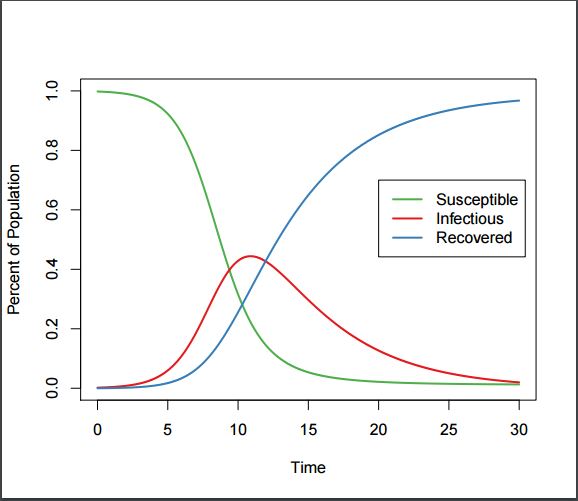
SIR Plot, showing typical categorization of a population into Susceptible, Infectious, and Recovered states.
Definitions¶
- Susceptible
- Individual is able to become infected.
- Exposed
- Individual has been infected with a pathogen, but due to the pathogen’s incubation period, is not yet infectious.
- Infectious
- Individual is infected with a pathogen and is capable of transmitting the pathogen to others.
- Recovered
- Individual is either no longer infectious, or “removed” from the population.
SI (Susceptible - Infectious) model¶
In this situation, people never leave the infectious state and have life-long infections. For example, herpes is a disease with life-long infectiousness. The dashed line shows how the model becomes an SIS (Susceptible - Infectious - Susceptible) model, where infection does not confer immunity (or there is waning immunity). Individuals have repeat or reoccurring infections, and infected individuals return to the susceptible state. For example, sexually transmitted diseases such as gonorrhea or chlamydia fall into this group.
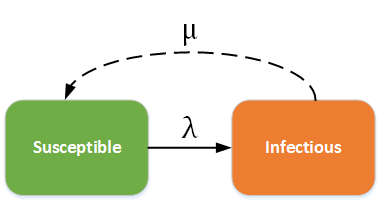
SI - SIS model
SIR (Susceptible - Infectious - Recovered) model¶
In this category, individuals in the recovered state gain immunity to the pathogen. For example, measles, mumps, rubella, and pertussis may be modeled using the SIR framework. The dashed line shows how the model becomes an SIRS (Susceptible - Infectious - Recovered - Susceptible) model, where recovery does not confer life-long immunity, and individuals may become susceptible again.
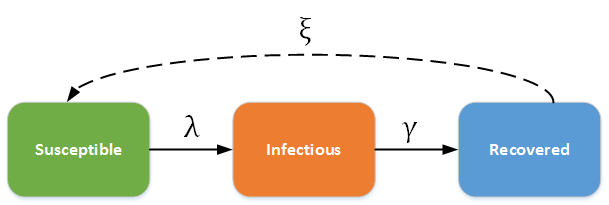
SIR - SIRS model
SEIR (Susceptible - Exposed - Infectious - Recovered) model¶
In this category, individuals experience a long incubation duration (the “exposed” category), such that the individual is infected but not yet infectious. For example chicken pox, and even vector-borne diseases such as Dengue Hemorrhagic fever have a long incubation duration where the individual cannot yet transmit the pathogen to others. The dashed line shows how the model becomes an SEIRS (Susceptible - Exposed - Infectious - Recovered - Susceptible) model, where recovered people may become susceptible again (recovery does not confer life-long immunity). For example, rotovirus and malaria are diseases with long incubation durations, and where infection only confers temporary immunity.
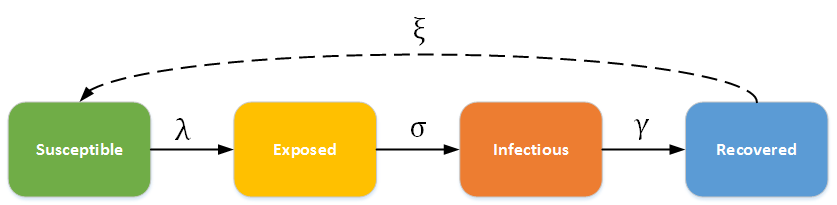
SEIR - SEIRS model
Fundamental concepts in epidemiology and disease modeling¶
- Basic reproductive number (R0)
The average number of secondary infections generated by the first infectious individual in a population of completely susceptible individuals. R0=S*L*
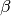 (where S = the number of susceptible hosts, L = length of infection, and
(where S = the number of susceptible hosts, L = length of infection, and 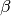 = transmissibility). When R0> 1,
disease will spread. It is essentially a measure of the expected or average outcome of transmission.
This is the threshold parameter used to determine whether or not an epidemic will occur, and determines:
= transmissibility). When R0> 1,
disease will spread. It is essentially a measure of the expected or average outcome of transmission.
This is the threshold parameter used to determine whether or not an epidemic will occur, and determines:- The initial rate of increase of an epidemic (the exponential growth phase).
- The final size of an epidemic (what fraction of susceptibles will be infected).
- The endemic equilibrium fraction of susceptibles in a population (=1/ R0).
- The critical vaccination threshold, which is equal to 1-(1/ R0), and determines the number of people that must be vaccinated to prevent the spread of a pathogen.
- Disability-adjusted life years (DALY)
- The number of years of life lost due to premature mortality plus the years lost due to disability while infected. Used to quantify the burden of disease.
- Epidemic
An outbreak of an infectious disease, such that a greater number of individuals than normal has the disease. Epidemics have very high R0 (Recall R0>1 for a disease to spread) and are often associated with acute, highly transmissible pathogens that can be directly transmitted. Further, pathogens with lower infectious periods create more explosive epidemics.
- To control epidemics, it is necessary to reduce R0. This can be done by:
- Reducing transmissibility.
- Decreasing the number of susceptibles (by vaccination, for example).
- Decreasing the mean number of contacts or the transmissibility, such as by improving sanitation, or limiting the number of interactions sick people have with healthy people.
- Reducing length of infectious period.
- To control epidemics, it is necessary to reduce R0. This can be done by:
- Force of infection (FoI)
- A measure of the degree to which an infected individual can spread infection; the per-capita rate at which susceptibles contract infection. Typically increases with transmissibility and prevalence of infection.
- Herd immunity
- Vaccines protect individuals, but also provide indirect protection to anyone those vaccinated people may have infected. The portion of the population that needs to be immunized in order to achieve herd immunity is P > 1 – (1/ R0), where P = proportion vaccinated * vaccine efficacy.
- Incidence (of a pathogen)
- The number of new cases or infections in a given time period.
- Immune
- Unable to become infected/infectious
- Prevalence (of a pathogen)
- The proportion of a population that is infectious at any given time.
- Transmissibility (
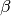 )
) - Also known as the effective contact rate, is the product of the contact rate and the probability of transmission per contact.
- Virulence
- The capacity of a pathogen to produce disease. It is proportional to parasitemia, or the number of circulating copies of the pathogen in the host. The higher the virulence (given contact between S and I individuals), the more likely transmission is to occur. However, higher virulence means contact may be less likely as infected hosts show more symptoms of the disease. There is a trade-off that occurs between high transmissibility and disease-induced mortality.